문제
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.
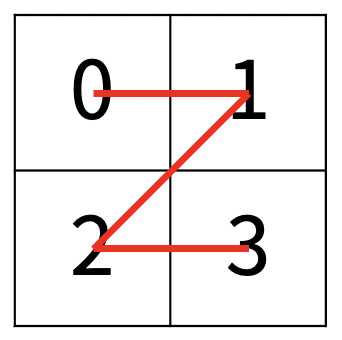
N > 1인 경우, 배열을 크기가 2N-1 × 2N-1로 4등분 한 후에 재귀적으로 순서대로 방문한다.
다음 예는 22 × 22 크기의 배열을 방문한 순서이다.
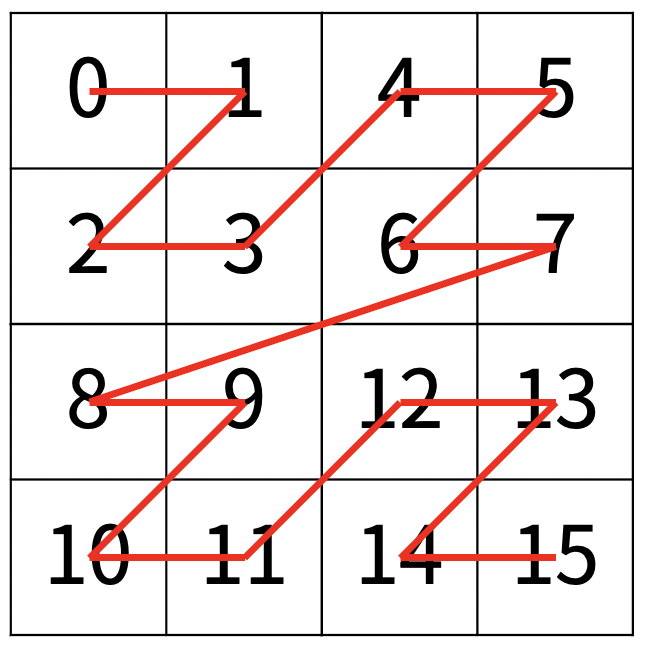
N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
다음은 N=3일 때의 예이다.
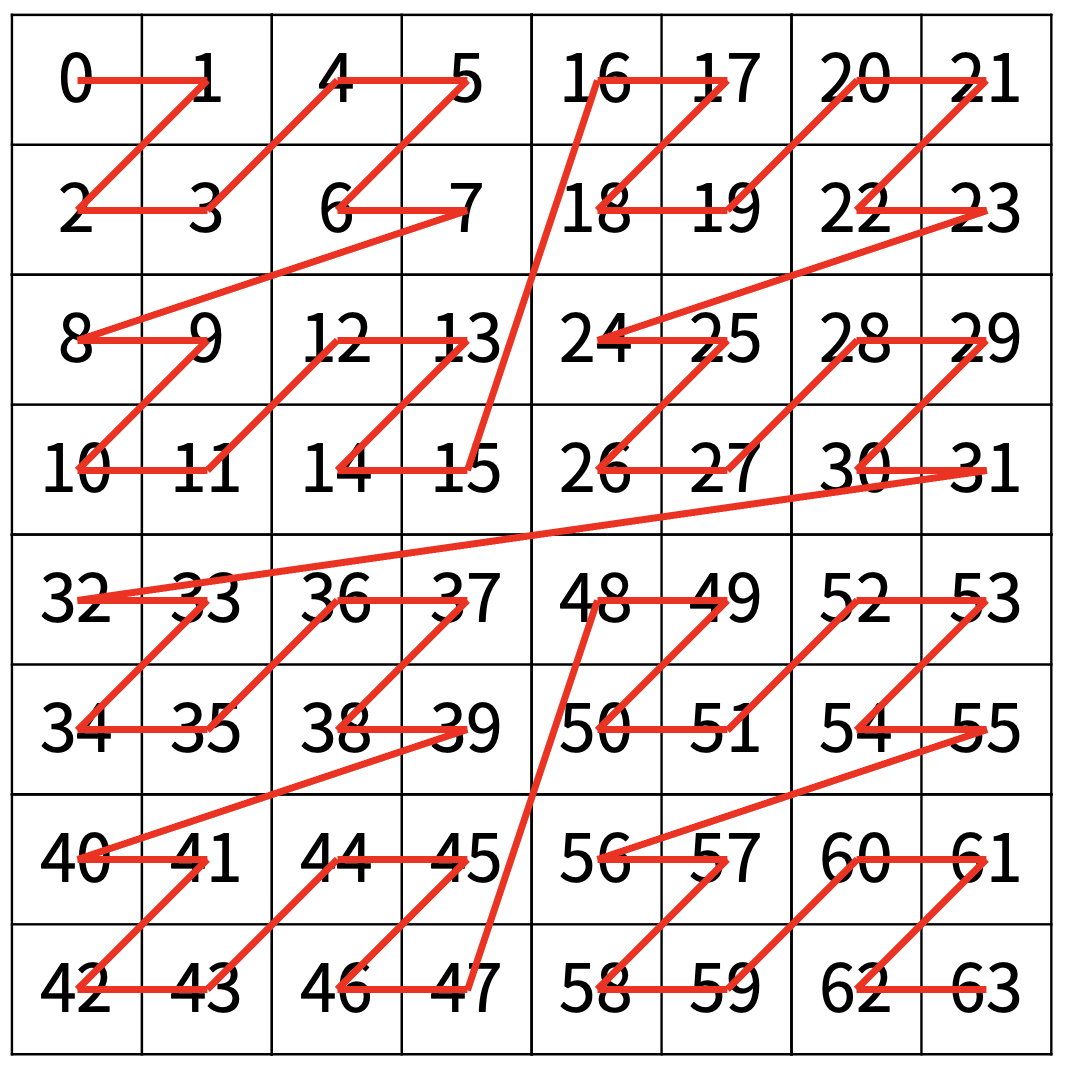
입력
첫째 줄에 정수 N, r, c가 주어진다.
출력
r행 c열을 몇 번째로 방문했는지 출력한다.
테스트 케이스
입력 1
3 4 5
출력 1
49
입력 2
10 2 9
출력 2
73
입력 3
2 1 2
출력 3
6
접근
처음에는 모든 맵 처음부터 다그리려 했는데, 아무래도 시간초과가 날 것 같아서,
분할 & 재귀를 이용하여 풀었습니다. (이렇게 저렇게 해보다가 2시간이나 걸려버린...)
제가 문제를 풀 수 있었던 핵심은 이렇습니다.
1. 맵이 나올 때마다 4등분한다.
2. 4등분했을때 첫값은 4^(n-1) * m (m=0,1,2,3)이다.
ex)아래 그림에서 4등분 했을때 각 맵의 첫 값은 0, 16, 32, 48 입니다.
즉, n이 3이므로
4^2 * 0 = 0;
4^2 * 1 = 16;
4^2 * 2 = 32;
4^2 * 2 = 48;
예상대로 값이 나옵니다.

이를 또 잘라 보겠습니다.
이번에는 n=2 입니다.
식은 4^(n-1) *m (m=0,1,2,3)
4 * 0 = 0;
4 * 1 = 4;
4 * 2 = 8;
4 * 3 = 12;

..이런식으로 계속 자르면 더 이상 자를 수 없을때 그 값이 답 입니다.
3. 사각형을 자른 뒤(4등분), r,c를 잘 조작하여 어느 사각형으로 이동할지 재귀인자를 설정합니다.
코드
import java.util.*;
import java.io.*;
public class Main_1074_Z {
static int N,R,C;
static int result;
public static void recursion(int n, int r, int c,int value) {
if(n == 0) {
result =value;
return;
}
int temp = (int)Math.pow(2, n);
int temp2 = temp/2;
if(r >=0 && r < temp2 ) {
//왼쪽위
if(c >= 0 && c < temp2) {
recursion(n-1,r,c,value+0);
}//오른쪽 위
else if(c >= temp2 && c < temp) {
recursion(n-1,r,c-temp2,value+(int)Math.pow(4, n-1));
}
}
else if(r >= temp2 && r < temp) {
//왼쪽 아래
if(c >= 0 && c < temp2) {
recursion(n-1,r-temp2,c,value+(int)Math.pow(4, n-1)*2);
}
//오른쪽 아래
else if(c >= temp2 && c < temp) {
recursion(n-1,r-temp2,c-temp2,value+(int)Math.pow(4, n-1)*3);
}
}
}
public static void main(String[] args) throws Exception {
// TODO Auto-generated method stub
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
R = Integer.parseInt(st.nextToken());
C = Integer.parseInt(st.nextToken());
recursion(N,R,C,0);
bw.write(String.valueOf(result));
br.close();
bw.flush();
bw.close();
}
}주의
시간초과 주의~!
'공부 정리 > 백준' 카테고리의 다른 글
| [백준] 자바 11659 구간 합 구하기4 (0) | 2022.03.15 |
|---|---|
| [백준] 자바 2630 색종이 만들기 (0) | 2022.03.14 |
| [백준] 자바 3040 백설 공주와 일곱 난쟁이 (0) | 2022.03.01 |
| [백준] 자바 10972 다음 순열 (0) | 2022.02.28 |
| [백준] 자바 2961 도영이가 만든 맛있는 음식 (0) | 2022.02.24 |




댓글